Question

Ms. Musto opened a new coffee shop. She recorded the number of customers she served between opening and noon for the first 20 days of business. Her results are shown on the graph.

Which line best fits the data?

Question 2 options:


y = 3x + 10


y = 2x + 20


y = 3x + 30


y = x + 20

Answer 1

The answer I believe is y=x+20

Answer 2

`y=2x+20`

Explanation:

If you take a look closer, you can see that the imaginary line that have to go through the center of all points has an approximate y-interception at 20. Pay attention, that this is an approximation. Also, you can observe that 10 or 30 are not close to the center of the points. So, we already discard the first and third choice.

Now, we need to decide if the slope is 2 or 3.

We can find the slope by using two points well defined, that is, points that are at specific locations. We can use (10, 45) and (15,55), and the formula of slopes

`m=(y_(2)-y_(1) )/(x_(2) -x_(1) )`

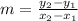
Replacing those points, we have

`m=(y_(2)-y_(1) )/(x_(2) -x_(1) )\\m=(55-45)/(15-10)\\ m=(10)/(5)\\ m=2`

So, we have the y-intercept at 2 (
`b=2)`, and the slope is
`m=2`.

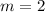The explicit form of a line would be

`y=mx+b\\y=2x+20`

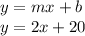
Therefore, the line that best fits is
`y=2x+20`