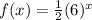Answer:
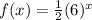
Explanation:
An exponential function is of the form
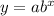 , where,
, where,
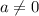 .
.
Now, if a > 0 and b > 1, then the exponential function represent exponential growth.
If a > 0 and 0 < b < 1, then the exponential function represent exponential decay.
Let us check each function now.
Option 1:
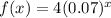
Here,
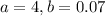
As 0.07 < 1, the function is exponential decay.
Option 2:
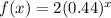
Here,
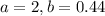
As 0.44 < 1, the function is exponential decay.
Option 3:
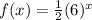
Here,
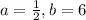
As 6 > 1, the function is exponential growth.
Option 4:
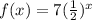
Here,
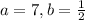
As
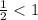 , the function is exponential decay.
, the function is exponential decay.
Therefore, the equation that represent exponential growth is