Answer:
A ) The value of x for the given circle with chords and center is 8.3
B) The circumference of circle with chords 1.2 cm and 0.5 cm is 4.082
Explanation:
Given two figures :
For Figure first
A circle with center y , having two chords FM and NM
FM = 5 x
MN = 2 x + 25
Now from theorem of circle ,
Chords equidistant from center of circle are equal in length
I.e distance of chord MN from center y and distance of FM from center y are equal
So, FM = MN
Or, 5 x = 2 x + 25
Or, 5 x - 2 x = 25
Or, 3 x = 25
∴ x =
 = 8.33
= 8.33
For figure second
The length of two adjacent chords of circle is 1.2 cm and 0.5 cm
Let the center of circle = O
Length of chord AB = 1.2 cm
Length of chord BC = 0.5 cm
As both chords are at 90° to each other
So The Length of diameter of circle AC =

Or, The Length of diameter of circle AC =
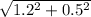
Or, The Length of diameter of circle AC =
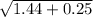
Or, The Length of diameter of circle AC =
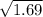
∴ The Length of diameter of circle AC = 1.3 cm
So, Circumference of circle =

Or, Circumference of circle = 3.14 × 1.3
∴ Circumference of circle = 4.082 cm
Hence,
A ) The value of x for the given circle with chords and center is 8.3
B) The circumference of circle with chords 1.2 cm and 0.5 cm is 4.082 Answer