Answer:
If X mile is the distance of the park from his home, then, X ≤ 65
Explanation:
As Alexandria wants to hike for 2 hours and can reach the speed of average 65 miles per hour to and from the park,
so , we get that she can hike for
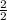 hour = 1 hour when going to the park from home.
hour = 1 hour when going to the park from home.
and if X mile is the distance of the park from his home, then
X ≤
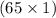
⇒ X ≤ 65