Question

Miguel wrote two equations. he thinks the two equations represent parallel lines. is he correct? explain why or why not.

-2x+6y=-42
y+10=1/3(x-3)

Answer 1

Yes, he is correct because both the lines have same slope.

Explanation:

Given:

The two equations are:

`-2x+6y=-42\\y+10=(1)/(3)(x-3)`

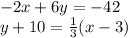
Two lines are parallel only if their slopes are equal.

So, let us write each equation in slope-intercept form
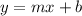`y=mx + b`, where,
`m` is the slope of the line.

Equation 1 is:

`-2x+6y=-42\\6y=2x-42\\y=(2)/(6)x-(42)/(6)\\y=(1)/(3)x-7`

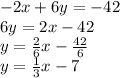
So, the slope of line 1 is
`m_(1)=(1)/(3)`

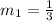
Now, equation 2 is:

`y+10=(1)/(3)(x-3)\\y+10=(1)/(3)x-3* (1)/(3)\\y+10=(1)/(3)x-1\\y=(1)/(3)x-1-10\\y=(1)/(3)x-11`

Therefore, slope of line 2 is,
`m_(2)=(1)/(3)`

∵
`m_(1)=m_(2)=(1)/(3)`

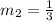
Therefore, both the lines are parallel to each other.