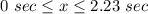Question

Jack was so frustrated with his slow laptop that he threw it out of his second story window. The height, h, of the laptop at time t seconds can be given by the equation h(t)= -16t^2 + 28t + 17. Assuming the laptop hits the ground below, find the domain of the function.

Answer 1

The domain of the function is the interval [0,2.23]

see the explanation

Explanation:

Let

t ----> the time in seconds

h(t) ----> the height of the laptop in units

we have

`h(t)=-16t^(2)+28t+17`

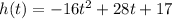
we know that

When the laptop hits the ground, the value of h(t) is equal to zero

so

For h(t)=0

`-16t^(2)+28t+17=0`

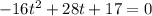
Solve the quadratic equation

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`-16t^(2)+28t+17=0`

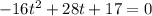
so

`a=-16\\b=28\\c=17`

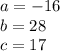
substitute in the formula

`x=\frac{-28(+/-)\sqrt{28^(2)-4(-16)(17)}} {2(-16)}`

`x=\frac{-28(+/-)√(1,872)} {-32}`

`x=\frac{-28(+/-)12√(13)} {-32}`

`x_1=\frac{-28(+)12√(13)} {-32}=-0.477`

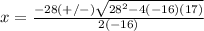
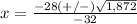
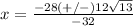
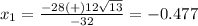
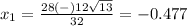`x_1=\frac{28(-)12√(13)} {32}=-0.477` ---> is not a solution

`x_2=\frac{-28(-)12√(13)} {-32}`

`x_2=\frac{28(+)12√(13)} {32}=2.23\ sec`

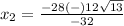
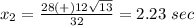
therefore

The domain of the function is the interval [0,2.23]

All real numbers greater than or equal to 0 seconds and less than or equal to 2.23 seconds

`0\ sec \leq x \leq 2.23\ sec`