Answer:
The correct option is C) 21.1 and 0.68
Explanation:
Consider the provided information.
The mean composite score was 21.1 with a standard deviation of 4.8. The ACT composite score ranges from 1 to 36, with higher scores indicating greater achievement in high school.
Therefore μ = 21.1 and σ = 4.8
It is given that the sample of 50 students;
Thus, sample size ( n ) = 50
According to the central limit theorem,
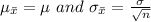
Therefore
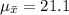
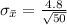
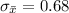
Hence, the correct option is C) 21.1 and 0.68