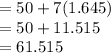Question

Assume that the random variable X is normally distributed, with mean ? = 50 and standard deviation ? = 7. Compute the following probabilities. Be sure to draw a normal curve with the area corresponding to the probability shaded.

P(56 < X < 68)

B- find the value of za.

z 0.02

C-assume that the random variable X is normally distributed, with mean ? = 50 and standard deviation ? = 7. Find each indicated percentile for X.

The 90th percentile

D-the graph of a normal curve is given. Use the graph to identify the values of ? and ?.

Answer 1

Explanation:

Given that the random variable X is normally distributed, with

mean = 50 and standard deviation = 7.

Then we have z=
`(x-50)/(7) is N(0,1)`

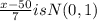
Using this and normal table we find that

a)
`P(56<x<68)\\= P(0.86<Z<2.57)\\=0.4949-0.3051\\=0.1898`

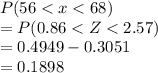
b) When z=0.02

we get

`x=50+0.02(7)=50.14`

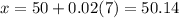
c) 90th percentile z value =1.645

90th percentile of X
`=50+7(1.645)\\= 50+11.515\\=61.515`