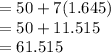Answer:
Explanation:
Given that the random variable X is normally distributed, with
mean = 50 and standard deviation = 7.
Then we have z=
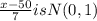
Using this and normal table we find that
a)
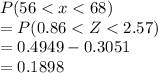
b) When z=0.02
we get
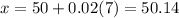
c) 90th percentile z value =1.645
90th percentile of X