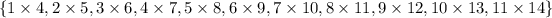Question

The length of a rectangle is 3 inches greater than its width. The perimeter is less than 54

inches. Describe the dimensions of the rectangle.

Answer 1

The dimensions of rectangle can anyone from the set
`\{1 * 4,2 * 5,3 * 6,4 * 7,5 * 8,6 * 9,7 * 10,8 * 11,9 * 12,10 * 13,11 * 14\}`

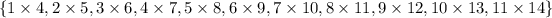
Solution:

Given that , The length of a rectangle is 3 inches greater than its width.

The perimeter is less than 54 inches.

Now, let the width of the rectangle be "n" inches. Then, the length of the rectangle will be n + 3 inches.

perimeter = 2(length + width)

Substituting the values, we get,

perimeter = 2(n + 3 + n) = 2 (2n + 3)

perimeter = 4n + 6

Now, we are given that, perimeter is less than 54

Then, perimeter < 54

4n + 6 < 54

4n < 54 – 6

4n < 48

n < 12

So, that, the width of the rectangle can be any value less than 12 inches.

Such that the values of width of rectangle are from 1 to 11

And corresponding length of rectangle are 1 + 3 to 11 +3 ⇒ 4 to 14

Thus Dimensions of rectangle can anyone from the set
`\{1 * 4,2 * 5,3 * 6,4 * 7,5 * 8,6 * 9,7 * 10,8 * 11,9 * 12,10 * 13,11 * 14\}`