Answer:
Hence the value of n should be 580.
Explanation:
Consider the provided information.
It is given that e = 0.05
p = 32% = 0.32
The confidence interval is 99%
for 99% CI critical Z = 2.580
We can calculate the sample size by using the formula.
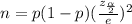
Substitute the respective values
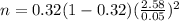
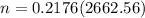

Hence the value of n should be 580.