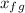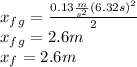Answer:
(a)

(b)
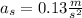
(c)
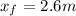
Step-by-step explanation:
(a) According to Newton's second law, the acceleration of a body is directly proportional to the force exerted on it and inversely proportional to it's mass.
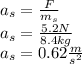
(b) According to Newton's third law, the force that the sled exerts on the girl is equal in magnitude but opposite in the direction of the force that the girl exerts on the sled:

(c) Using the kinematics equation:
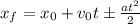
For the girl, we have
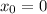 and
and
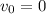 . So:
. So:
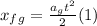
For the sled, we have
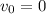 . So:
. So:
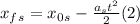
When they meet, the final positions are the same. So, equaling (1) and (2) and solving for t:

Now, we solve (1) for