Question

(Based on Q14) The International Coffee Association has reported the mean daily coffee consumption for U.S. residents as 1.65 cups. Assume that a sample of 38 people from a North Carolina city consumed a mean of 1.84 cups of coffee per day, with a standard deviation of 0.85 cups. In a two-tail test at the 0.05 level, could the residents of this city be said to be significantly different from their counterparts across the nation?

Answer 1

We fail to reject null hypothesis.

Explanation:

Consider the provided information.

The mean daily coffee consumption for U.S. residents as 1.65 cups. Assume that a sample of 38 people from a North Carolina city consumed a mean of 1.84 cups of coffee per day, with a standard deviation of 0.85 cups.

`H_0:\mu=1.65`

`Ha0:\mu\\eq 1.65`

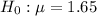
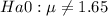
According to the formula:
`t=(\bar x-\mu)/((\sigma)/(√(n)))`

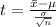
Substitute n=38, x = 1.84, μ = 1.65 and σ = 0.85 in above formula.

`t=(1.84-1.65)/((0.85)/(√(38)))`

`t=1.38`

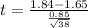
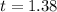
Now find degree of freedom (df)

df=n-1=37

α = 0.025

The appropriate t value with df =37 and α = 0.025 is 2.026

The t value which we calculated is less than 2.026, Hence, we fail to reject null hypothesis.