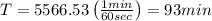Answer:
A.
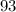 min
min
Step-by-step explanation:
 = mass of earth = 6.0 x 10²⁴ kg
= mass of earth = 6.0 x 10²⁴ kg
 = Radius of earth = 6400 km = 6.4 x 10⁶ m
= Radius of earth = 6400 km = 6.4 x 10⁶ m
 = Altitude above earth = 400 km = 0.4 x 10⁶ m
= Altitude above earth = 400 km = 0.4 x 10⁶ m
Radius of orbit of the space station around earth is given as
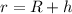

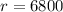 km
km
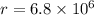 m
m
 = Time period of orbit of space station
= Time period of orbit of space station
Here we can use Kepler's third law which is given as
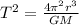
Inserting the above values
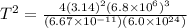
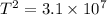
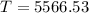 sec
sec