Question

A dumbbell-shaped object is composed by two equal masses, m, connected by a rod of negligible mass and length r. If I₁ is the moment of inertia of this object with respect to an axis passing through the center of the rod and perpendicular to it and I₂ is the moment of inertia with respect to an axis passing through one of the masses, it follows thata. l₁ = l₂. b. l₁ > l₂. c. l₂ > l₁.

Answer 1

option C

Step-by-step explanation:

Mass of m is on the both the side of the dumbbell

moment of inertia of the object when the axis is passing through the center and perpendicular to it

distance from the center be r/2

I₁ = mr₁² + mr₂²

I₁ =
`m(r^2)/(4) + m(r^2)/(4)`

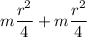
I₁ =
`(mr^2)/(2)`

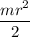
when the axis pass through one mass

I₂ = mr₁² + mr₂²

r₁ = 0 r₂ = r

I₂ = m(0)² + m(r)²

I₂ = m r²

hence, I₂ > I₁

correct answer is option C