The given system of equations represent a single line with positive slope. Option C is correct
Solution:
Given, a system of equations which are shown below,
3y − 5x = 15 ⇒ (1)
6y − 10x = 30 ⇒ (2)
When we observe the above equations, when first equation is multiplied with 2, it results in second equation
Eqn 1 multiplied with "2" , we get
⇒ 6x - 10x = 30 ⇒ eqn 3
If we notice eqn 2 and eqn 3 are same.
Which means the two line equations represents the same line.
Now let us find the slope of line.
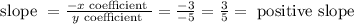
So, the line has a positive slope. Thus the given system of equations represent a single line with positive slope. So option C is correct.