Question

A choreographer uses a number line to position dancers for a ballet. Dancers A and B have coordinates 5 and 23, respectively. Find the coordinate for the following dancer based on the given location.

Dancer E stands at a point that divides the line segment from Dancer A to Dancer B in a ratio of 2 to 1.

Dancer E is
units from Dancer A, so the coordinate for Dancer E is
.

Answer 1

Dancer E is I think 12 units to Dancer A I think

Explanation:

Answer 2

Dancer E is 12 units from Dancer A, so the coordinate for Dancer E is 17.

Explanation:

Distance from Dancer A to Dancer B.

AB = 23 - 5 = 18 units

Distance from Dancer A to Dancer E.

`\begin{array}{lrcll}(1) & (AE)/(EB) & = & (2)/(1) & \\\\(2) & AE + EB & =  & 18 \\(3) & AE & = & 2EB & \text{Multiplied each side of (1) by EB} \\(4) & 2EB + EB & = &18 & \text{Substituted (3) into 2} \\\end{array}`

`\begin{array}{lrcll}& 3EB & = & 18 & \text{Simplified} \\&EB & =  & (18)/(3) & \text{Divided each side by 3} \\\\(5)&EB& = & \mathbf{6} &\text{Simplified}\\\end{array}`

`\begin{array}{lrcll}& AE + 6 & = & 18 & \text{Substituted (5) into (2)} \\& AE& = & 18 - 6 & \text{Subtracted 6 from each side} \\& AE& = & \mathbf{12} & \text{Simplified} \\\end{array}`

`\textbf{AE = 12}`

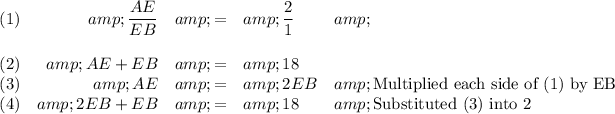
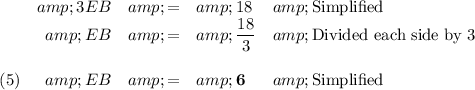
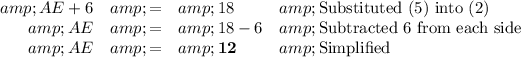
Dancer E is 12 units from Dancer A, so the coordinate for Dancer E is 5 + 12 = 17.