Answer:
the engine cool to 40
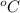 at 14.07 minutes
at 14.07 minutes
Step-by-step explanation:
Given information
T(5) = 70
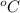
 = 100
= 100
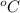
C = 15
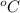
Newton's law of cooling :
T(t) = C + (
 - C)
- C)

where
T(t) = temperature at any given time
C = surrounding temperature
 = initial temperature of heated object
= initial temperature of heated object
k = cooling constant
to find the the time when the engine will be cooled down to 40
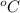 , we first need to find the cooling constant, k
, we first need to find the cooling constant, k
when t = 5, T(5) = 70
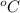
so,
T(t) = C + (
 - C)
- C)

T(5) = 15 + (100 - 15)
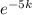
70 = 15 + (85)
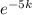
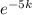 = (70 - 15) / 85
= (70 - 15) / 85
-5k = ln (55/85)
k = - ln (55/85) / 5
k = 0.087
thus, we have the eqaution
T(t) = 15 + (85)
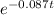
now we can determine the time when T(t) = 40
40 = 15 + (85)
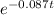
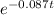 = (40-15)/85
= (40-15)/85
-0.0087t = ln (25/85)
t = - ln (25/85)/0.087
t = 14.07 minutes