Question

A 2012 Gallup survey of a random sample of 1014 American adults indicates that American families spend on average $151 per week on food. The report further states that, with 95% confidence, this estimate has a margin of error of ±$7.

(a) This confidence interval is expressed in the following form: "estimate ± margin of error." What is the range of values (lower bound, upper bound) that corresponds to this confidence interval?

(b) What is the parameter captured by this confidence interval? What does it mean to say that we have "95% confidence" in this interval?

Answer 1

a.[144;158]$

b. The parameter estimated is the population mean of the weekly expenses on the food of American families.

Explanation:

Hello!

The study variable for this problem is "Weekly expenses on food spent by an American family"($)

For a sample n=1014 American families the corresponding sample mean is x[bar]=$151

It is stated that for the 95%CI the margin of error is ±$7

a.

The confidence interval that estimates the population mean is constructed as the "estimator ± margin of error" for example, under a Standard Normal distribution the formula for the confidence interval is:

[x[bar]±
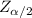`Z_(\alpha/2)`*(δ/√n)]

For the sample taken it is:

[151±7]

The inferior limit is 144$

The superior limit is 158$

b.

The parameter estimated is the population mean of the weekly expenses on the food of American families.

The confidence level of an interval is the probability under which it is built. This probability indicates that if they build 100 confidence intervals, we expect 95 to contain the value of the population mean we are trying to estimate.

I hope you have a SUPER day!