Question

A comet is first seen at a distance of d astronomical units from the Sun and it is traveling with a speed of q times the Earth’s speed. Show that the orbit of the comet is hyperbolic, parabolic, or elliptic, depending on whether the quantity q 2d is greater than, equal to, or less than 2, respectively

Answer 1

To solve this problem it is necessary to take into account the concepts of Gravitational Force and Kinetic Energy.

The kinetic energy is given by the equation:

`F= \frac{mv^2}2`

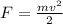
La energía gravitacional por,

`F=(GM_cm)/(d)`

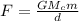
Where m is the mass, v is the velocity, G the gravitational constant
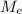`M_e` the mass of the earth, m the mass of the sun and d the distance ..

The sum of the energies, we must be a total energy

`E= \frac{mv^2}2+(GM_em)/(d)`

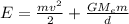
By the type of orbit we know that

E> 0 is a hyperbolic orbit

E = 0 is a parabolic orbit

E <0 is a closed orbit.

In the case of hyperbolic orbit

E>0

`(mq^2)/(2)-(GM_em)/(d)>0\\(qv^2_e)/(2)>(GM_em)/(d)\\q^2d>2(GM_e)/(v^2_e)\\q^2d>2`

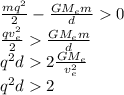
The case of the comet is a closed orbit, so,

E<0

`\frac{mv^2}2+(GM_em)/(d)<0\\(mq^2v^2_e)/(2)<(GM_cm)/(d)\\q^2d<2(GM_e)/(v^2_e)`

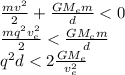
For parabolic orbit

E=0

`(mv^2_eq^2)/(2)-(GM_cm)/(d)=0\\(v^2_eq^2)/(2)=(GM_c)/(d)\\q^2d=2(GM_e)/(v^2_e)\\q^2d=2`

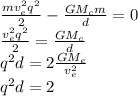
For the sun and the earth

`(m_ev_e^2)/(r)=(GM_em_e)/(r^2)`

`v^2_e=(GM_e)/(r)\\(GM_e)/(v_e)=r`

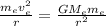
where
`R \approx 1AU`

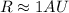
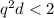`q^2d<2` For elliptical orbit