Question

A beetle with a mass of 15.0 g is initially at rest on the outer edge of a horizontal turntable that is also initially at rest. The turntable, which is free to rotate with no friction about an axis through its center, has a mass of 95.0 g and can be treated as a uniform disk. The beetle then starts to walk around the edge of the turntable, traveling at an angular velocity of 0.0700 rad/s clockwise with respect to the turntable.

(a) With respect to you, motionless as you watch the beetle and turntable, what is the angular velocity of the beetle? Use a positive sign if the answer is clockwise, and a negative sign if the answer is counter-clockwise.
? rad/s

(b) What is the angular velocity of the turntable (with respect to you)? Use a positive sign if the answer is clockwise, and a negative sign if the answer is counter-clockwise.
? rad/s

(c) If a mark is placed on the turntable at the beetle's starting point, how long does it take the beetle to reach the mark again?

Answer 1

a) w₁ = 0.070 rad/s , b) w₂ = -0.022 rad/s and c) t = 6.83 s

Step-by-step explanation:

To solve this problem let's use the conservation of angular momentum; The system is the beetle plus the disk, so the torques are internal and the angular momentum is preserved. Let's write at two initial points, before beginning the movement and when the insect moves

Initial

L₀ = 0

Final

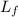`L_(f)` = L₁ + L₂

Where L₁ and L₂ are the beetle and disk angular moments respectively

L₁ = I₁ w₁

L₁ = m r² w₁

L₂ = I₂ w₂

I₂ = ½ M r²

L₂ = ½ M r² w₂

L₀ =
`L_(f)`

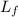
0 = m r² w₁ + ½ M r² w₂

m r² w₁ = - ½ M r² w₂

w₂ = - 2m /M w₁

a) The angular velocity of the beetle is w₁ = 0.070 rad / s

b) let's calculate the angular velocity of the disk

m = 15.0 g (1 kg / 1000g) = 0.0150 kg

M = 95.0 g = 0.0950 kg

w₂ = - 2 0.015 / 0.095 0.070

w₂ = -0.022 rad / s

c) In this case we must be careful since both: beetle and disc move, therefore if they leave the same point when they find the mark they have turned the same angle again, the disc moves starting from initial angle 2π

The angular acceleration for both is zero

θ₁ = w₁ t + ½ α t2

θ₂ = θ₀ + w₂ t * ½ α₂ t

θ₁ = w₁ t

θ₂ = θ₀ + w₂ t

θ₁ = θ₂

w₁ t = θ₀ + w₂ t

t (w₁ - w₂) = θ₀

t = θ₀ / (w₁ - w₂)

t = 2π / (0.070 - (-0.022))

t = 6.83 s