Question

Pedro can drive 2 times as fast as Pablo can ride his bicycle. If it takes Pablo 2 hours longer than Pedro to travel 72 miles, how fast can Pablo ride his bicycle?

Answer 1

Pablo can ride his bicycle with speed of 18 miles per hour

Solution:

Given, Pedro can drive 2 times as fast as Pablo can ride his bicycle.

Let the speed of Pablo be "n" miles per hour

Then the speed of the Pedro will be "2n" miles per hour

Now, If it takes Pablo 2 hours longer than Pedro to travel 72 miles,

We have to find how fast can Pablo ride his bicycle?

The formula for speed is given as:

`\text { distance }=\text { speed } * \text { time }`

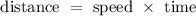
Let the time taken by Pedro to travel 72 miles be "t" hours, then time taken by Pablo will be "t + 2" hours

In case of Pablo:

`\begin{array}{l}{72 \text { miles }=\text { speed } * (t+2) \text { hour }} \\ {\rightarrow 72=n *(t+2) \rightarrow(1)}\end{array}`

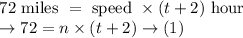
In case of Pedro:

`\begin{array}{l}{72 \text { miles }=\text { speed } * \text { thours }} \\ {\rightarrow 72=2 n * t \rightarrow(2)}\end{array}`

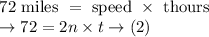
Then, equate both (1) and (2)

`\begin{array}{l}{n *(t+2)=2 n * t} \\\\ {\rightarrow t+2=2 * t} \\\\ {\rightarrow t+2=2 t} \\\\ {\rightarrow 2 t-t=2} \\\\ {\rightarrow t=2}\end{array}`

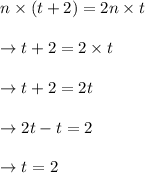
Now, substitute t = 2 in (2)

`\begin{array}{l}{\rightarrow 72=2 n * 2} \\\\ {\rightarrow 72=4 n} \\\\ {\rightarrow n=18}\end{array}`

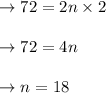
Hence, the speed of Pablo is 18 miles per hour.