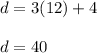Question

a group of hikers park there trail head and hike into the forest to a campsite. The next morning they head out on a hike from their campsite walking at a steady rate. The graph shows their distance in miles d from the car on the day of their hike after h hours. How many miles will the campers be from their car after 12 hours?

Answer 1

Answer: The campers will be
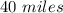`40\ miles` from their car after 12 hours.

Explanation:

The missing graph is attached.

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" the y-intercept.

We can pick two points on the line graphed and substitute the coordinates into this formula to find the slope:

`m=(y_2-y_1)/(x_2-x_1)`

Choosing the points (0,4) and (2,10), we get:

`m=(4-10)/(0-2)=3`

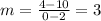
We can susbstitute the point (0,4) and the slope into
`y=mx+b` and solve for "b":

`4=3(0)+b\\\\b=4`

Then, the equation of this line is:

`y=3x+4`

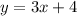
Since the distance in miles is represented on the y-axis and the time in hours is represented on the x-axis. we can rewrite the equation as:

`d=3h+4`

Finally, in order to calculate the distance in miles that the campers will be from their car after 12 hours, we need to subsitute
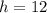`h=12` into the equation and evaluate. Then we get:

`d=3(12)+4\\\\d=40`