Question

A marine surveyor uses a rangefinder and a compass to locate a ship and an island in the vicinity of the coast on which she stands. The rangefinder indicates that the island is 393 ft from her position and the ship is 515 from her position. Using the compass, she finds that the ship's azimuth is 332 degrees and that of the island is 48 degrees. What is the distance between the ship and the island.

Answer 1

The distance between the ship and the island is
`d\approx 567.23 \ft`.

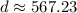Explanation:

The ship's azimuth is the direction measured as an angle from the north.

You should draw a diagram of the situation.

From the information given we know two distances and the angle between them and we want to find the distance between the ship and the island.

To find the distance between the ship and the island we can use the Law of Cosines.

If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of cosines states:

`c^2=a^2+b^2-2ab\cdot cos(C)`

This law is useful for finding: the third side of a triangle when we know two sides and the angle between them like in this case.

The angle is

`\theta=48\°+(360-332)\°=76\°`

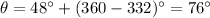
And the distance is given by

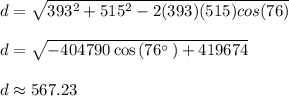`d=√(393^2+515^2-2(393)(515)cos(76)) \\\\d=\sqrt{-404790\cos \left(76^(\circ \:)\right)+419674}\\\\d\approx 567.23 \ft`.