Answer:
The selling price that will maximize profit is $56.
Explanation:
Given : It costs 12 dollars to manufacture and distribute a backpack. If the backpacks sell at x dollars each, the number sold, n, is given by
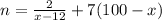
To find : The selling price that will maximize profit ?
Solution :
The cost price is $12.
The selling price is $x
Profit = SP-CP
Profit = x-12
The profit of n number is given by,
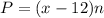
Substitute the value of n,
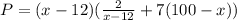
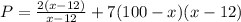
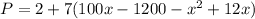
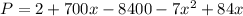
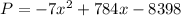
Derivate w.r.t x,
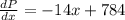
Put it to zero for critical point,
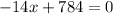
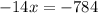
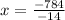
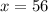
Derivate again w.r.t x, to determine maxima and minima,
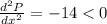
It is a maximum point.
Therefore, the selling price that will maximize profit is $56.