Question

A survey of 350 students is selected randomly on a large campus. They are asked if they use a laptop in class to take notes. Suppose that based on the survey, 140 of the 350 students responded "yes."

A. What is the value of the sample proportion ^p?

B. What is the standard error of the sample Proportation?

C. Construct an approximate 95% confidence interval for the true proportion p by taking +- SEs from the sample proportion.

Answer 1

A. The value of the sample proportion is 0.4

B. The standard error of the sample proportion is 0.02619

C. 0.3487 ≤ p ≤ 0.4513

Explanation:

The value of the sample proportion p' is calculated as:

`p'=(x)/(n) = (140)/(350)=0.4`

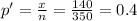
Where x is the number of success in the sample or the number of students that use a laptop in class to take notes and n is the size of the sample or 350 students.

On the other hand, the standard error SE of the sample proportion is calculated as:

`SEs=\sqrt{(p'(1-p'))/(n)}`

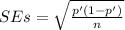
so, replacing the values, we get:

`SE=\sqrt{(0.4(1-0.4))/(350)}=0.02619`

Finally, an approximate 95% confidence interval for the true proportion p is calculate as:

`p'-z_(\alpha/2) SEs \leq p\leq p'+z_(\alpha/2) SEs`

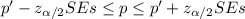
Where 1-α is equal to 95%, so
`z_(\alpha/2)` is equal to 1.96. Then, replacing the values we get:

`0.4-1.96(0.02619) \leq p\leq 0.4+1.96(0.02619)`

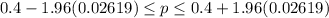
0.4 - 0.0513 ≤ p ≤ 0.4 + 0.0513

0.3487 ≤ p ≤ 0.4513