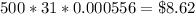Question

The function below represents the annual interest Alexander earns on a savings account. Identify the term that represents the amount of time that the money is accruing interest. f(x) = 500(1 + 0.02)x

Answer 1

The term that represents the amount of time that the money is accruing interest in the given function f(x) = 500(1 + 0.02)x is 'x'.

Step-by-step explanation:

The term that represents the amount of time that the money is accruing interest in the given function is 'x'.

In the function f(x) = 500(1 + 0.02)x, the variable 'x' represents the amount of time in years that the money is accruing interest. It determines the exponential growth of the savings account balance over time.

For example, if x is equal to 1, it means the money is accruing interest for one year. If x is equal to 5, it means the money is accruing interest for five years.

Answer 2

X represents the time, in this function.

Step-by-step explanation:

1) Since in Alexander's savings account the Interest is also compounded, then this function is properly written this way:

`A=P(1+(r)/(n))^(nt)\Rightarrow A=500(1+(0.2)/(1))^(t)`

`f(x)=500(1+0.02)^(x)`

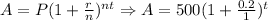
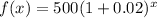
Replacing A for f(x) this function tells us that for a given period (x). This savings account with a principal of $500, and 20% interest compounded annually will provide us how much he earns.

Further explanations

3) In case you want to calculate the accrues (accumulated) interest of this saving account, after having found the time, you have to know whether it is daily weekly or monthly accrued, etc.

For example:

Daily interest accrued (accumulated)= 20% (0.2) : 360 days =

`(0.2)/(360)=0.000556`

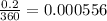
Supposing 31 days after the investment, Alexander will have from his $500 this interest payable:

`500 * 31 *0.000556=\$8.62`