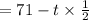Question

grandpa joe started getting shorter in 2002 (let x=0). every year after that he shrunk 1/2 an inch. in 2008 he was 68 inches tall. write an equation to model this situation.

Answer 1

The equation to model the situation is
`=71-t * (1)/(2)`

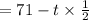
Solution:

Given, Grandpa Joe started getting shorter in 2002 (let x=0)

Height shrunken =
`(1)/(2)`

Present Height in 2008 = 68 inches

Now, let the number of years lived after 2002 be “t”

Then, present height = height in 2002 – number of years lived x height shrunken

`\text { Present height }=\text { height in } 2002-t * (1)/(2)`

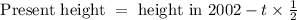
Since from 2002 to 2008 , it is 6 years span, so t = 6

`\text { Present height in } 2008=\text { height in } 2002-6 * (1)/(2)`

68 inches = height in 2002 – 3 inches

Height in 2002 = 68 + 3 = 71 inches

So, grandpa is 71 inches tall in 2002

Then, our equation will be modified as present height
`=71-t * (1)/(2)`