Question

A spring of spring constant k = 340 Nm-1 is used to launch a 1.5-kg block along a horizontal surface by compressing the spring by a distance of 18 cm. If the coefficient of sliding friction between the block and the surface is 0.25, how far does the block slide?

Answer 1

The block slides 1.5m

Step-by-step explanation:

To solve this problem we need the concepts relate to work energy, work done, frictional force and normal force.

We know for definition that,

`W = \Delta KE = F*d`

Where W is the work and \Delta KE the change in Kinetic Energy, F the force and d the distance.

`W = (1)/(2)kx^2_f-(1)/(2)kx^2_i`

The expression is relate to the Hook's law where F=kx, being k the elastic constant and x the displacement of the object.

We know as well that Frictional Force is given by

`F_f = \mu N = \mu mg`

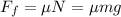
Where
`\mu` is the coefficient of friction, m the mass and g the gravity acceleration.

We can now solve the problem. Using the first equation we have,

`W = (1)/(2)kx^2_f-(1)/(2)kx^2_i`

Using the second form for work,

`F_f*d = (1)/(2)kx^2_f-(1)/(2)kx^2_i`

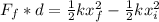
Here we know that
`x_i` is zero and F_f is equal to
`\mu` mg

`(\mu mg)*d = (1)/(2)kx^2_f`

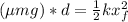
Re-arrange for d,

`d= \frac{{(1)/(2)kx^2_f}}{\mu mg}`

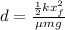
Replacing the values we have,

`d=  (340*18*10^(-2))/(2*(0.25)(1.5)(9.8))`

`d = 1.498m \approx 1.5m`

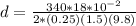
The block slides 1.5m