Question

At Lisa’s printing Company LLC there are two kinds of printing presses model a witch can print 70 bucks per day and model B which can print 55 bucks per day the company owns 14 total printing presses and this allows them to print 905 bucks per day how many of each type of price do they have?

Answer 1

9 machines of model A and 5 machines of model B working in a day to print 905 bucks.

Solution:

Given that

Model A can print 70 bucks per day

Model B can print 55 bucks per day

Total number of printing presses = 14

Total number of bucks printed by machines of Model A and Model B in 1 day = 905

Let assume number of printing presses of model A = "y"

As total 14 printing presses are there and "y" are of model A, so remaining that is (14 – y) will be of model B.

Number of bucks printed by 1 machine of model A in one day = 70

So number of bucks printed by "y" machine of model A is given as:

`\begin{array}{l}{=y * \text { Number of bucks printed by } 1 \text { machine of model } \mathrm{A} \text { in one day }} \\\\ {=y * 70=70 \mathrm{y}}\end{array}`

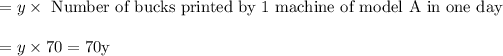
Number of bucks printed by 1 machine of model B in one day = 55

So number of bucks printed by (14 –y) machine of model B is given as:

`\begin{array}{l}{=(14-y) * \text { Number of bucks printed by } 1 \text { Machine of model } B \text { in one day }} \\\\ {=(14-y) * 55=770-55 y}\end{array}`

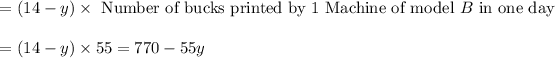
Also given that Total number of bucks printed by machines of Model A and Model B in 1 day = 905

Total number of bucks printed by machines of Model A and Model B in 1 day = number of bucks printed by "y" machine of model A + Number of bucks printed by (14 –y) machine of model B

`\begin{array}{l}{=>905=70 \mathrm{y}+(770-55 \mathrm{y})} \\\\ {=>905=70 \mathrm{y}+770-55 \mathrm{y}} \\\\ {=>905-770=70 \mathrm{y}-55 \mathrm{y}} \\\\ {=>135=15 \mathrm{y}} \\\\ {=>\mathrm{y}=(135)/(15)=9}\end{array}`

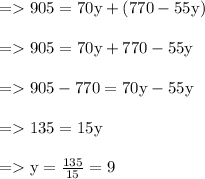
Number of printing presses of model A = y = 9

Number of printing presses of model B =(14- y) = 14 – 9 = 5

Hence 9 machines of model A and 5 machines of model B working in a day to print 905 bucks.