Question

An unknown radioactive element decays into non-radioactive substances. In 440 days the radioactivity of a sample decreases by 74 percent.

(a) What is the half-life of the element?
half-life: (days)

(b) How long will it take for a sample of 100 mg to decay to 91 mg?
time needed: (days)

Answer 1

a) The half life of the element is 231 days.

b) It is going to take around 31.5 days for a sample of 100 mg to decay to 91 mg.

Explanation:

The radioactivity of the sample can be modeled by the following exponential equation:

`R(t) = R(0)e^(-rt)`

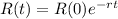
In which t is the time in days, r is the decay rate and
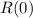`R(0)` is the initial radioactive percentage.

We have that:

In 440 days the radioactivity of a sample decreases by 74 percent.

This means that
`R(440) = 0.26R(0)`.

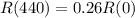This helps us find r.

`R(t) = R(0)e^(-rt)`

`0.26R(0) = R(0)e^(-440r)`

`e^(-440r) = 0.26`

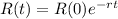
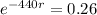
Applying ln to both sides.

`\ln{e^(-440r)} = ln(0.26)`

`-440r = -1.347`

`r = 0.003`

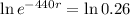
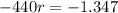
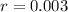
(a) What is the half-life of the element?

This is t when
`R(t) = 0.50R(0)`

`R(t) = R(0)e^(-rt)`

`0.50R(0) = R(0)e^(-0.003t)`

`e^(-0.003t) = 0.5`

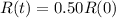
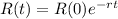
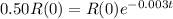
Again, we apply ln to both sides of the equality.

`\ln{e^(-0.003t)} = ln(0.5)`

`-0.003t = -0.693`

`t = 231`

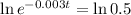
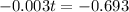
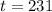
The half life of the element is 231 days.

(b) How long will it take for a sample of 100 mg to decay to 91 mg?

This is t when
`R(t) = 0.91R(0)`

`R(t) = R(0)e^(-rt)`

`0.91R(0) = R(0)e^(-0.003t)`

`e^(-0.003t) = 0.91`

`\ln{e^(-0.003t)} = ln(0.91)`

`-0.003t = -0.09`

`t = 31.44`

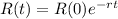
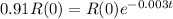
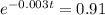
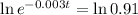
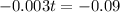
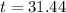
It is going to take around 31.5 days for a sample of 100 mg to decay to 91 mg.