Answer:
![\frac{x^(2) -\sqrt[3]{y}}{x+y}=9](https://img.qammunity.org/2020/formulas/mathematics/middle-school/e4bd8yaein7bh5ycwzkd1fjiv1qfcuvz3d.png)
Explanation:
we know that
The quotient means, divide the numerator by the denominator
In this problem
1) The numerator is "the square of a number minus the cubed root of another number"
Let
x ----> a number
y ----> another number
The algebraic expression of the numerator of the quotient is
![x^(2) -\sqrt[3]{y}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/713a0x91nv8lz8v96xfpqaigo14vl2yayu.png)
2) The denominator is "the sum of those two numbers"
so
The algebraic expression of the denominator of the quotient is
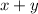
3) The quotient of the square of a number minus the cubed root of another number and the sum of those two numbers is nine
Equate the quotient to the number 9
so
we have
![\frac{x^(2) -\sqrt[3]{y}}{x+y}=9](https://img.qammunity.org/2020/formulas/mathematics/middle-school/e4bd8yaein7bh5ycwzkd1fjiv1qfcuvz3d.png)