Question

Assume that all​ grade-point averages are to be standardized on a scale between 0 and 6. How many​grade-point averages must be obtained so that the sample mean is within 0.006 of the population​ mean? Assume that a 99​% confidence level is desired. If using the range rule of​thumb, σ can be estimated as Range/4=6-0/4 = 1.5. Does the sample size seem​practical?

Answer 1

416025 grade-point averages must be obtained so that the sample mean is within 0.006 of the population​ mean. But this size too big and is not practical.

Explanation:

Minimum required grade-point averages can be found using the formula

N≥
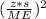`((z*s)/(ME) )^2` where

• N is the sample size
• z is the corresponding z-score in 99% confidence level (2.58)
• s is the standard deviation (1.5)
• ME is the margin of error (0.006)

Putting these numbers in the formula we get

N≥
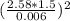`((2.58*1.5)/(0.006) )^2` =416025