Consider two particles A and B. The angular position of particle A, with constant angular acceleration, depends on time according to
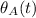
=θ₀+ω₀t+12αt². At time t=t₁, particle B, which also undergoes constant angular acceleration, has twice the angular acceleration, half the angular velocity, and the same angular position that particle A had at time t=0.How long after the time t₁ does the angular velocity of B have to be to equal A's?