The time of death was approximately 31.2 minutes before 10:30 AM.
How to determine the time?
We employed Newton's Law of Cooling in order to determine time;
This law is expressed by the formula:
![\[ T(t) = T_a + (T_0 - T_a) \cdot e^(-kt) \]](https://img.qammunity.org/2020/formulas/physics/college/mdr2zody5ur6apb9nkbce4n1y4psuq5e25.png)
In this equation:
 is the temperature at time
is the temperature at time
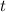 ,
,
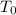 is the initial temperature of the body,
is the initial temperature of the body,
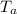 is the ambient temperature (room temperature),
is the ambient temperature (room temperature),
 is a constant, and
is a constant, and
 is the base of the natural logarithm.
is the base of the natural logarithm.
Given the specifics:
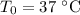 (normal body temperature),
(normal body temperature),
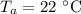 (room temperature),
(room temperature),
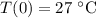 (temperature at 10:30 AM),
(temperature at 10:30 AM),
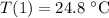 (temperature one hour later),
(temperature one hour later),
We aimed to find
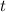 , representing the time of death when the body temperature reached 37°C.
, representing the time of death when the body temperature reached 37°C.
![\[ 37 = 22 + (27 - 22) \cdot e^(-kt) \]](https://img.qammunity.org/2020/formulas/physics/college/pwns02eer3bxe4b0awa5wp9zcbhcpza3pp.png)
![\[ 15 = 5 \cdot e^(-kt) \]](https://img.qammunity.org/2020/formulas/physics/college/nil8eolq83pchjgcda23a6v72fa2rdg87k.png)
![\[ e^(-kt) = 3 \]](https://img.qammunity.org/2020/formulas/physics/college/bhw6xrsi63dw3te8p5doyk4bq5dc1ha7so.png)
![\[ -kt = \ln(3) \]](https://img.qammunity.org/2020/formulas/physics/college/80fet28ey2b4po0o1269h6a73i9k80x5ky.png)
![\[ t = -(\ln(3))/(k) \]](https://img.qammunity.org/2020/formulas/physics/college/30qpckmr7tt7m6l3c8qc767bn80e6r2k4a.png)
Determining the value of
 involved using the information from the initial temperature drop:
involved using the information from the initial temperature drop:
![\[ 24.8 = 22 + (27 - 22) \cdot e^(-k \cdot 1) \]](https://img.qammunity.org/2020/formulas/physics/college/sgld90dvzdq28ow7u0sbdkwt3e6cb9ol51.png)
![\[ 2.8 = 5 \cdot e^(-k) \]](https://img.qammunity.org/2020/formulas/physics/college/li8ekkdsj1ww3l7rv7mzut75hibo9zkx2k.png)
![\[ e^(-k) = 0.56 \]](https://img.qammunity.org/2020/formulas/physics/college/7s3ecktsjsguvwjz4frd7n8l6cfmmt0228.png)
![\[ -k = \ln(0.56) \]](https://img.qammunity.org/2020/formulas/physics/college/5bexfi01sb852w8unj2rw0dsiqvcyc0975.png)
![\[ k \approx 0.576 \]](https://img.qammunity.org/2020/formulas/physics/college/is5shkemjtz451p8bv2ktwftw00w5bn78l.png)
Substituting this
 value back into the equation for
value back into the equation for
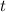 :
:
![\[ t \approx -(\ln(3))/(0.576) \]](https://img.qammunity.org/2020/formulas/physics/college/zaup9eywyua8n4egv2kzh3hixvrvthda1s.png)
![\[ t \approx 0.52 \text{ hours} \]](https://img.qammunity.org/2020/formulas/physics/college/kjjf76fqi5nx2z1aqgyhim5eajajutm34c.png)
To convert this to minutes, multiply by 60:
![\[ t \approx 31.2 \text{ minutes} \]](https://img.qammunity.org/2020/formulas/physics/college/gvle5resnowo7pr8dc9bevp41byj2yu11l.png)
Therefore, the time of death was approximately 31.2 minutes before 10:30 AM.