Answer:
2.268
Step-by-step explanation:
The concepts that we need to use here for give a solution are Drag coefficient and drag force.
Drag force is given by,
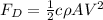
Where,
c is the drag coefficient
 is the density
is the density
A cross sectional area
V the velocity.
Our values for this problem are divided for Passenger and Driver.
For Jet are:
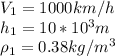
For prop-driven are:

From the problem we need to assume that
 and
and
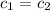 , THEN
, THEN
Applying to each case the Drag force equation we have,
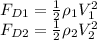
The ratio between the two force is,

Therefore the force experienced by a Jet pilot under these conditions is 2,268 times greater than that of a prop-driven