Question

Abby, Deborah, Mei-Ling, Sam, and Roberto work in a firm's public relations office. Their employer must choose two of them to attend a conference in Paris. To avoid unfairness, the choice will be made by drawing two names from a hat (This is an SRS of size 2.)(a) Write down all possible choices of two of the five names. This is the sample space. (Parts b-d of this problem are based on the possible choices listed in part a (choice of 2 names).(b) The random drawing makes all choices equally likely. What is the probability of each choice?(c) What is the probability that Mei-Ling is chosen?(d) What is the probability that neither of the two men (Same and Roberto) are chosen

Answer 1

a) Ω = { {Abby, Deborath}, {Abby, Mei-Ling}, {Abby, Sam}, {Abby,Roberto}, {Deborah, Mei-Ling}, {Deborah, Sam}, {Deborah, Roberto}, {Mei-Ling, Sam}, {Mei-Ling, Roberto}, {Sam, Roberto} }

b) 0.1

c) 0.4

d) 0.3

Explanation:

a) The sample space must contain every possible combination of two names. Since we dont care about the order of the chosen names, we can describe every element of the sample space as a subset of 2 elements of the set {Abby, Deborah, Mei-Ling, Sam, Roberto}. That subset will represent the names of the chosen persons. With this in mind, we conclude that the sample space is

Ω = { {Abby, Deborath}, {Abby, Mei-Ling}, {Abby, Sam}, {Abby,Roberto}, {Deborah, Mei-Ling}, {Deborah, Sam}, {Deborah, Roberto}, {Mei-Ling, Sam}, {Mei-Ling, Roberto}, {Sam, Roberto} }

b) The cardinality of the sample space Ω is 10. Since all choices are equally likely, any choice will have probability
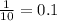`(1)/(10) = 0.1` , because the 10 of them combined must add up 1.

c) We need to find all possible choices that includes Mei-Ling, those will be our favourable cases. The amount of favourable cases must be divided to the total amount of cases (the cardinality of Ω) in order to obtain the probability of Mei-Ling being chosen. Mei-Ling is included on 4 choices (one for each of her partners), this means that she has a probability of
`(4)/(10) = 0.4` to being chosen.

d) We have 3 favourable cases ,the choices {Abby, Deborah}, {Abby, Mei-Ling} and {Deborah, Mei-Ling}, which neither of them contain a man. By dividing that number to the total number of cases, we obtain a probability of
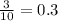`(3)/(10) = 0.3` that neither of the two men are chosen