Question

You are a sales rep, and receive phone messages that 2 of your 4 major customers need to talk to you about making a major purchase. Unfortunately, neither one identified themselves or left a callback number. So you will call them back in no particular order until you find one of the interested customers.Let X= {1, 2, 3, 4} stand for which of your calls finally talks to one of the interested customers.a) Write down a table of the probability mass function p(x) = P(X = x) for which call reaches the first interested customer.b) Calculate the expected number of calls E(X) you will have made when you talk to the first interested customer.

Answer 1

a) the probability mass function p(x) = P(X=x) is:

`p(1)=0.5`

`p(2)=0.333`

`p(3)=0.166`

`p(4)=0`

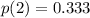
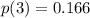
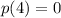
b) The expected number of calls E(X) you will have made when you talk to the first interested customer is 1.667 calls

Explanation:

The probability that you will talk with one of the interest customers at the first call is:

`p(1)=(2)/(4) =0.5`

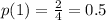
Because, you have 4 possibles customers and 2 of them are interested.

Also, the probability that you will talk with one of the interest customers at the second call is:

`p(2)=(2)/(4)*(2)/(3)=0.333`

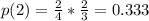
Because, in the first call you are going to talk with one customer that it is not interested, so you have 4 possibles customers and 2 of then are not interested. Then, for the second call, you are going to talk with one customer that it is interested, so, now, you have 3 possibles customers and 2 of them are interested.

At the same way, the probability that you will talk with one of the interest customers at the third call is:

`p(3)=(2)/(4)*(1)/(3)*(2)/(2)=0.166`

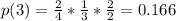
Finally, taking into account that there are 4 customers and 2 of them are interested, the maximum number of calls for find the first customer interested is 3, so P(4) is zero.

So, the probability mass function p(x) = P(X=x) is:

`p(1)=(2)/(4)=0.5`

`p(2)=(2)/(4)*(2)/(3)=0.333`

`p(3)=(2)/(4)*(1)/(3)*(2)/(2)=0.166`

`p(4)=0`

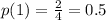
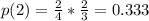
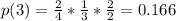
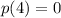
Then, the expected value is calculated as:

`E(x)=x_1p(x_1)+x_2p(x_2)+... + x_np(x_n)`

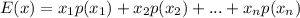
Where
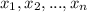`x_1, x_2,...,x_n` are the possible values of the variable and
`p(x_1), p(x_2),...,p(x_n)` are their respectives probabilities.

Therefore, the expected number of calls that you will have made when you talk to the first interested customer is:

E(x)=1(0.5) + 2(0.333) + 3(0.166) + 4(0) = 1.667