2 Answers

Hurturk · Answer 1 · 2020-05-17T04:32:57+0000

The coordinates of the point C on the x-axis so that AC + BC is a minimum is; C(5.5, 0)

The steps used to solve for the coordinates of the point C can be presented as follows;

Let (x, 0) represent the coordinates of the point C on the axis

The coordinates of the point A is (3, 6), and the coordinates of the point B is (8, 4), therefore;

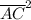$\overline{AC}^2$ = (3 - x)² + (6 - 0)²

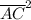$\overline{AC}^2$ = x² - 6·x + 45

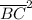$\overline{BC}^2$ = (8 - x)² + (4 - 0)²

(8 - x)² + (4 - 0)² = x² - 16·x + 80

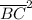$\overline{BC}^2$ = x² - 16·x + 80

Where AC + BC is a minimum, we get;
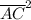$\overline{AC}^2$ +
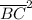$\overline{BC}^2$ is also a minimum, which indicates that at the minimum value, we get;

x² - 6·x + 45 + x² - 16·x + 80 = 2·x² - 22·x + 125

d(2·x² - 22·x + 125)/dx = 0

d(2·x² - 22·x + 125)/dx = 4·x - 22

x = 22/4

x = 5.5

Therefore the coordinates of the point C is (5.5, 0)

Please log in or register to add a comment.