Answer:
a) Slope of line 1 = (2/3)
b) Slope of line 2 = (-3/2)
c) Two lines are perpendicular.
Explanation:
Here, let the points of line 1 are A(1,0) and B(7,4)
Let the points of line 2 are A(7,0) and B(3,6)
Now for any two points, the slope m of the line is given as :
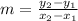
⇒Slope of the line AB =
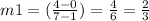
or, m1 = 2/3
and Slope of the line PQ =
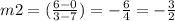
or, m2 = -3/2
Now, TWO LINERS ARE SAID TO BE PERPENDICULAR if
m1 x m2 = -1 :with heir respective slope m1 and m2
Here,
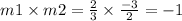
⇒ SLOPE OF AB x SLOPE OF PQ = -1
Hence, Line AB is perpendicular to the line PQ.