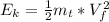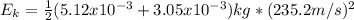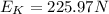Answer:
velocity
a).
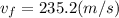
direction
b).
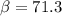
kinetic energy
c).
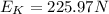
Step-by-step explanation:
Those kind of question have two typical questions inside to response the final velocity and the direction finding the angle and finally the kinetic energy so each the information you need can find there so
a).
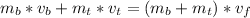
solve to vf
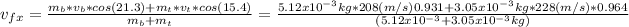
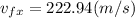
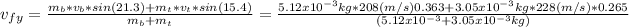
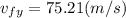
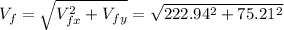
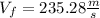
b).
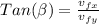
solve to β
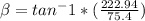
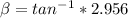
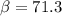
c).
Final kinetic energy