Question

Find the measure of Angle A

Answer 1

A) 55°

Explanation:

All the angles of a triangle add up to 180°, therefore, in order to determine A, we can write an equation for this with our given values

x + 62 + 87 + x + 45 = 180

With this, we can simply solve from here

x + 62 + 87 + x + 45 = 180

2x = -14

x = -7

And since the original question asks for the measure of angle A, we input this value into the expression given for A

let x = -7

x + 62

= -7 +62

= 55°

Therefore, angle A is 55°

Answer 2

The correct answer is option A) 55⁰.

Step-by-step explanation:

As we know that the sum of interior angles of triangle is 180⁰.

So, adding all the given sides and subtracting to 180⁰, to find the value of x.

`\begin{gathered}\quad\longrightarrow{\rm{Sum \: of \: all \: angles = {180}^(\circ)}}\\\\\quad{\longrightarrow{\tt{(x + 62) + ({45}^( \circ)) + (87 + x) = {180}^(\circ)}}}\\\\\quad{\longrightarrow{\tt{(x + x) + (62 + 45 + 87)= {180}^(\circ)}}}\\\\\quad{\longrightarrow{\tt{(2x) + (107 + 87)= {180}^(\circ)}}}\\\\\quad{\longrightarrow{\tt{(2x) + (194)= {180}^(\circ)}}}\\\\\quad{\longrightarrow{\tt{(2x)= {180} - 194}}}\\\\\quad{\longrightarrow{\tt{(2x)= - 14}}}\\\\\quad{\longrightarrow{\tt{2x= - 14}}}\\\\\quad{\longrightarrow{\tt{x= ( - 14)/(2)}}}\\\\\quad{\longrightarrow{\tt{\underline{\underline{x = - 7}}}}}\end{gathered}`

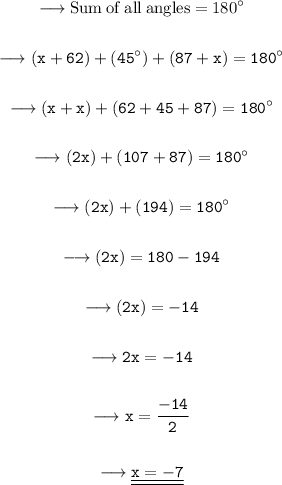
Hence, the value of x is -7.

`\begin{gathered}\end{gathered}`

Now, we know the value of x. So, calculating the measurement of angle A.

`\begin{gathered}\qquad{\leadsto{\tt{A = x + 62}}}\\\\\qquad{\leadsto{\tt{A = - 7 + 62}}}\\\\\qquad{\leadsto{\tt{\underline{\underline{A = {55}^( \circ)}}}}}\end{gathered}`

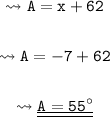
Hence, the measurement of angle A is 55⁰.

`\rule{300}{2.5}`