Answer:
(a) n=1 → E= -1.96x10⁻¹⁷ J
n=3 → E= -2.18x10⁻¹⁸ J
(b) λ = 11.4 nm
Step-by-step explanation:
(a) To find the energies needed to remove an electron from the n=1 state and n=3 state in the Li²⁺ ion, we need to use the Rydberg equation for energy change:
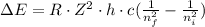
where ΔE: is the energy change, R: is the Rydberg constant, Z: is the atomic number, h: is the Planck constant, c: is the speed of light, nf: is the final state of the electron and ni: is the initial state of the electron.
To remove an electron from the state n=1 means that ni=1 and nf=∞, so the energy is:
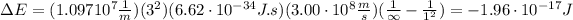
Similarly, to remove an electron from the state n=3 means that ni=3 and nf=∞, hence the energy is:

(b) To calculate the wavelength of the emitted photon in a transition from n=3 to n=1 we can use the Rydberg equation:
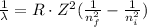
The transition is ni=3 and nf=1, therefore the wavelength of the emitted photon is:

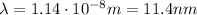
I hope it helps you!