Answer:
Part a)
all cars will travel equal distance before it stops
Part b)
Car F will have maximum work done by friction
Step-by-step explanation:
Part a)
As we know that the friction on Each car is given as
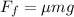
now the deceleration is given as
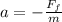
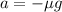
so the deceleration is independent of the mass of the car
now the distance to stop the car is given as
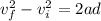
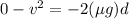
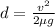
so all cars will travel equal distance before it stops
Part b)
Work done by friction force is given as

so we have
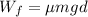
so most massive car will have maximum work done done by friction
so Car F will have maximum work done by friction