Answer:

Step-by-step explanation:
To solve this problem we need to apply the Kepler's third law, which say,
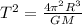
Where ,
T= Period
R = Radius
G =Gravitational constant
M = Mass
We have all that values, then replacing,
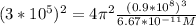
Solving for M,
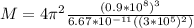

Note that
 is used because was provided the value of the diameter, not the radius which is equal to the half.
is used because was provided the value of the diameter, not the radius which is equal to the half.