Question

A (A+60.0) kg construction worker is standing on an 18.0 kg plank. The plank is (3.50+B) m long and it is suspended by vertical cables at each end. If the worker stands 2.80 from the right end of the plank, what is the tension in right cable? Give your answer in newtons (N) and with 3 significant figures.

Answer 1

The force at right side is 1058N

Step-by-step explanation:

The concept that we need to use to give a solution to this problem are the Static Equation where the force and torque do not experience an acceleration.

Our values are:

`m_1 = 60Kg\\m_2 = 18Kg\\L = 3.5m\\d = 2.8m`

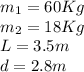
We have two tension from the wire, at left and right, then making sum we have

`\sum F = 0`

`T_L+T_R-mg=0`

`T_L+T_R = (60)(9.8)`

`T_L+T_R = 588N`

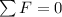
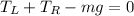
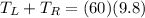
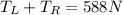
We can do now a sum of moments at right side, then

`\sum T = 0`

`mg*2.8+T_L*3.5=0`

`(60)(9.8)+T_L*3.5=0`

`T_L= -470.4N`

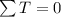
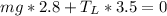
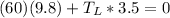
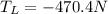
Replacing in the first equation,

`T_R+T_L=588N`

`T_R-470N=588N`

`T_R = 1058.4`

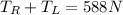
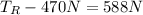
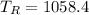
Therefore the force at right side is 1058N