Question

Police arrive at a murder scene at 3 : 30 AM and immediately record the​ body's temperature which was 90degrees°F. At 5:30 ​AM, after thoroughly inspecting and fingerprinting the​ area, they again took the temperature of the body which had dropped to 85degrees°F. The temperature of the crime scene has remained at a constant 70degrees°F. Determine when the person was murdered.​(Assume that the victim was healthy at the time of death. That​ is, assume that the temperature of the body at the time of death was 98.6degrees°​F.) The person was murdered at ? . ​(Do not round until the final answer. Then round to the nearest minute as​needed.)

Answer 1

The person was murdered at 11.40 PM

Explanation:

Given information :

Initial body temperature,
`T_(0)` = 90
`^(o)F`

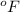
Police arrive at a murder scene at 3 : 30 AM, at 5.30 AM (120 minutes), temperature of the body had dropped to 85
`^(o)F`.

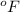T(120) = 85
`^(o)F`

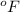
The temperature of the crime scene, C = 70
`^(o)F`

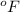
to determine the time of the murderer, we can use the Newton's lau of cooling:

T(t) = C + (
`T_(0)` - C)
`e^(-kt)`

where

T(t) = temperature at any given time

C = surrounding temperature

`T_(0)` = initial temperature of heated object

k = cooling constant

thus

T(t) = C + (
`T_(0)` - C)
`e^(-kt)`

T(120) = 70 + (90 - 70)
`e^(-120k)`

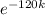
85 = 70 + 20
`e^(-120k)`

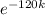
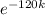`e^(-120k)` = (85-20) / 70

-120 k = ln (65/70)

k = - ln (65/70) / 120

= 0.00062

so we have the cooling equation

T(t) = 70 + (
`T_(0)` - 70)
`e^(-0.0062t)`

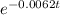
The temperature at the time of the death is 98.6
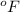`^(o)F` which was the initial temperature of the person murdered, the temperature dropped to T(t) = 85
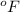`^(o)F` , now we can find the time of him being murdered.

T(t) = 70 + (98.6 - 70)
`e^(-0.0062t)`

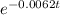
85 = 70 + 28.6
`e^(-0.0062t)`

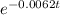
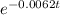`e^(-0.0062t)` = (85- 28.6)/70

-0.00062t = ln ((85- 28.6)/70)

t = - ln ((85- 28.6)/70)/ 0.00062

t = 350 minutes

therefore, the preson being murdered 350 minutes (5 hours 50 minutes) before 5.30, which was 11. 40 PM