The circle equation in standard form:
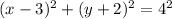
The circle equation in general form:
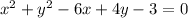
Solution:
Given that, center of a circle is (3, -2) and radius = 4.
We have to find the standard and general form of the circle.
Finding standard form:
The standard form of circle is
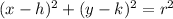
where (h, k) is center and r is radius.
So the standard form of circle is
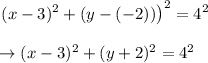
Finding general form:
Now, we just have to expand the standard form to get the general form.
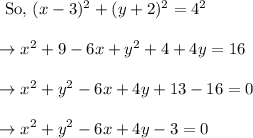
Hence the standard and general form are found out