Question

What is the area of a triangle with vertices at

(0, −2) ,(8, −2) , and ​ (9, 1) ?
Enter your answer in the box

( there is no provided image )

Answer 1

The area of a triangle with vertices at (0, −2) ,(8, −2) and ​(9, 1) is 12 square units

Solution:

Given, vertices of the triangle are A(0, -2), B(8, -2) and C(9, 1).

We have to find the area of the given triangle.

The area of triangle when vertices are given is:

`\text { Area of triangle }=(1)/(2)\left|x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right|`

`\text { Where, }\left(x_(1), y_(1)\right),\left(x_(2), y_(2)\right),\left(x_(3), y_(3)\right) \text { are vertices of the triangle. }`

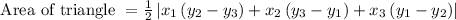
Here in our problem,

`\left(\mathrm{x}_(1), \mathrm{y}_(1)\right)=(0,-2),\left(\mathrm{x}_(2), \mathrm{y}_(2)\right)=(8,-2) \text { and }\left(\mathrm{x}_(3), \mathrm{y}_(3)\right)=(9,1)`

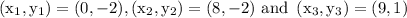
Now, substitute the above values in the formula:

`\text { Area of triangle }=(1)/(2)\left|x_(1)\left(y_(2)-y_(3)\right)+x_(2)\left(y_(3)-y_(1)\right)+x_(3)\left(y_(1)-y_(2)\right)\right|`

`\begin{array}{l}=(1)/(2) \\\\ 0+8(1+2)+9(2-2) \\\\ 0+24+0 \\\\ {=(24)/(2)} \\\\ {=12 \text { square units }}\end{array}`

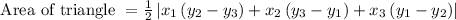
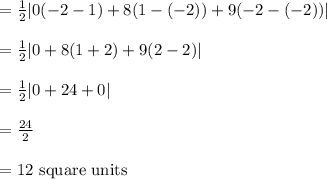
Hence, the area of the triangle is 12 square units.