Answer:
v' = 1.5 m/s
Step-by-step explanation:
Given that,
Mass of the car, m = 2010 kg
Speed of the car, v = 2.53 m/s
The car passes under a loading chute and gravel falls vertically into it for 3.25 s at the rate of 423 kg/s. Mass loaded during this time, m' = 1374.75 kg
Let v' is the speed of car after the loading is completed. Using the conservation of momentum to find it.

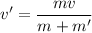
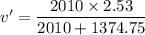
v' = 1.5 m/s
So, the speed of the car after the loading is completed is 1.5 m/s. Hence, this is the required solution.